Speaker
Description
Particle-in-cell (PIC) numerical simulations are widely used for the numerical modeling of plasma physics problems. These simulations are used primarily, but not exclusively, to study the kinetic behavior of the particles. For example, we used this method for numerical simulations of physics in linear particle accelerators [1,2].
The main idea of the method is to describe the plasma as a set of electrons and ions, which are modeled as discrete entities that move in continuous fields that are calculated on a computational mesh. The calculation of the motion of each particle is defined by electromagnetic fields. In our case, we use our modification of the finite-difference time-domain (FDTD) method as a discretization technique. A de-tailed description of the numerical method and scheme parallelization can be found in 3.
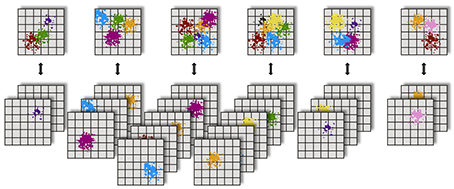
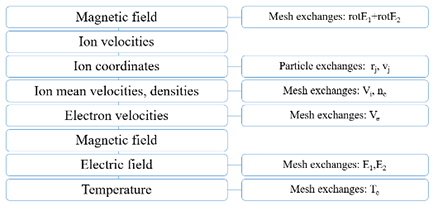
Figure 1 and 2 are briefly shows particle-domain decomposition and block-scheme of the algorithm for a one-time step. In our code, we apply a hybrid decomposition, divid-ing the computational domain along the z-axis into subdomains and assigning a group of processes to each subdomain. Within each group, particles are distributed almost uniformly: this uniformity is ensured by the even distribution of particles at the start, during the injection, and the exchanges by approximately equal quantities of particles with random processes of neighboring groups. A master processor of each group provides 3D arrays of the electromagnetic fields to his group and then gathers 3D arrays of the densities and mean velocities. During the Eulerian stage, the computations and the corresponding data exchanges with the ghost node values be-tween neighbor processes are performed only by the master group processes.
2 Vectorization
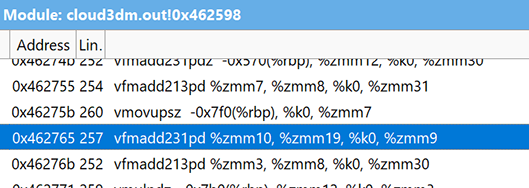
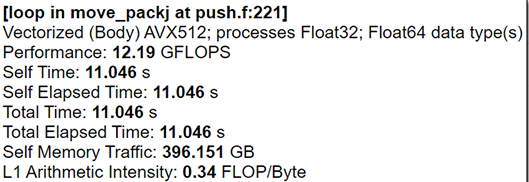
In our previous works 4, we used AVX512 intrinsics for numerical algorithm realization. However, the result of this approach is architecture-dependent code. At this moment, we are writing C++ or Fortran codes with different tricks that help the compiler build effective AVX512 code. In the case of our plasma physics solver, we have two of the “heaviest” functions which calculate particle data and density. For the autovectorization, we changed our mathematical expressions to ax+bx+c view. All division operations have been moved to separate operations. This approach helps the compiler to build FMA instructions using ZMM AVX-512 registers (see Fig.3 and Fig.4).

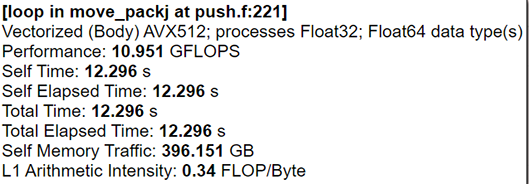
We also need to find data size parameters and particle pack size for better per-formance because of the specific particle-domain decomposition. Our tests showed that particle pack size can speed up particle data calculations function by up to 16% (see Fig.5 and Fig. 6) on the same data set.
Acknowledgments. This work was supported by the Russian Science Foundation (project 19-71-20026).
References
1. Chernykh, I., Kulikov, I., Vshivkov, V., Genrikh, E., Weins, D., Dudnikova, G., Cher-noshtanov, I., Boronina, M.: Energy Efficiency of a New Parallel PIC Code for Numeri-cal Simulation of Plasma Dynamics in Open Trap. Mathematics, 10, 3684 (2022).
2. Chernoshtanov, I.S., Chernykh, I.G., Dudnikova, G.I., Boronina M.A., Liseykina, T.V., Vshivkov, V.A. Effects observed in numerical simulation of high-beta plasma with hot ions in an axisymmetric mirror machine. Journal of Plasma Physics, 90, 2, 905900211 (2024).
3. Boronina, M.A., Chernoshtanov, I.S., Chernykh, I.G. et al: Three-Dimensional Model for Numerical Simulation of Beam-Plasma Dynamics in Open Magnetic Trap. Loba-chevskii J Math 45, 1–11. doi:10.1134/S1995080224010074 (2024)
4. Glinsky B., Kulikov I., Chernykh I., Weins D., Snytnikov A., Nenashev V., Andreev A., Egunov V., Kharkov E. The Co-design of Astrophysical Code for Massively Parallel Supercomputers. Lecture Notes in Computer Science, 10049, pp.342-353. DOI: 10.1007/978-3-319-49956-7_27 (2016)

